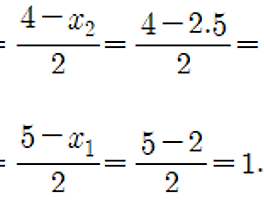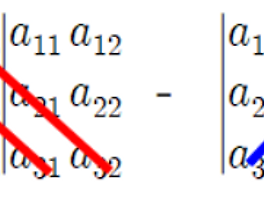반응형
안녕하세요. 수치해석에서 이용되는 방법들 중에 '이분법'과 '가위치법'에 대한 간략한 설명입니다. 참고하시어 학습하시는 데에 도움이 되면 좋겠습니다. 우선, 이분법을 먼저 설명하고 다음으로 가위치법에 대해 설명해보겠습니다.
1) 이분법(bisect)
이분법은 말 그대로 이등분으로 분해한다는 말입니다. 함수의 근을 모를 때 근이 있다고 판별할 수 있는 것이 함숫값 2개의 곱입니다. 함수값 2개를 구해서 그것의 곱이 (-) 라면, 그 사이에 근이 적어도 한 개 이상 존재한다는 개념을 사용한 것입니다. 그리고 이분법의 말 그대로 이분(두개로 나누어)하여 근의 위치를 찾아가는 방법입니다. 그리고 수치해석이라는 것 자체가 근을 모르는 상태에서 근을 찾아가는 방식을 말하는 것이기 때문에 다양한 방법들이 모두 '반복법'에 기초하여 근을 찾게 됩니다. 이분법도 마찬가지로 근이 위치할 것 같은 곳을 계속적으로 2개의 구간으로 나누어가면서 찾아가는 방식입니다. 아래의 수식으로 표현해보겠습니다.
우선, 다음과 같은 그래프가 있다고 가정하겠습니다. 저희는 아직 이 그래프를 표현하는 함수의 근을 모르는 상태입니다. 그래서 그래프적인 방법을 통하여 대략적인 근의 위치를 파악한 다음 아래와 같이 이분법을 예시로 근의 위치를 추적해보겠습니다.
.png)
(그래프 사진 출처 : Chapra의 응용수치해석 3판)
위 그래프를 보시면, 'First iteration'이라는 곳을 봐주시길 바랍니다. 여기서 첫번째 계산이 이루어진다는 말입니다. 그래서 x'l, x'u가 정의됩니다. (이때, l은 lower로 x의 작은 값을 표현하고, u는 upper로 x의 큰 값을 표현하는 것입니다. 이 때의 x'l과 x'u의 값이 그래프를 보시는 것처럼 한쪽은 음수, 한쪽은 양수가 되어 두 개의 함수값의 곱이 음수(-)가 됩니다. 앞서 말했듯이, 두 개의 함수값의 곱이 마이너스일 경우에는 둘 사이에 적어도 하나 이상의 근이 존재한다고 말씀드렸습니다. 수식으로 표현하면 다음과 같습니다.
.png)
여기서 이제, 처음의 x'l과 x'u 사이에 x'r이라는 점을 추가해주는 것이 이분법입니다. 위에서 'Second iteration'이라고 표현된 것의 우측 1차원 선을 보시게되면, 첫번째 계산에서 이분하여 구한 x'r이 다시 x'l이 되신 것을 알 수 있습니다. 이것의 계산은 다음과 같이 진행된 것입니다.
.png)
이해가 되시나요? 처음에 가정한 x'l과 x'u의 함숫값을 곱해보니 0보다 작아서 이 구간 내에 적어도 한 개 이상의 근이 존재하기 때문에, 그 구간을 이분하여 x'r을 구하게 됩니다. 그리고 다시 3)번에서와 같이 함숫값을 곱해보고 0보다 작은 구간을 찾아서 거기서의 근을 찾아내기 위해서 추적하는 것입니다. 따라서 5)번에서와 같이 기존의 x'l은 사라지고 x'r이 새로운 x'l값으로 변환되고, 기존의 x'u는 큰 값이므로 다음 계산의 x'u로 그대로 넘어가게 됩니다.
요약하자면, 이분법은 초기의 가정값 2개(x'l, x'u)가 필요하고 그 구간 내에 근이 존재할 것 같으면, 구간을 2등분하여 구한 새로운 값(x'r)과 비교하여 다시 다음 계산으로 구간을 좁혀나가는 것입니다. 따라서, 구간이 계산을 반복할 때마다 1/2로 줄어들게되며, 계속적으로 근의 위치를 추적할 수 있습니다.
단, 특이한 함수의 경우에는 근을 찾지 못하는 경우도 있다는 점을 상기시켜드립니다. 위 경우처럼 연속이며 부드러운 곡선에서 일반적으로 근을 찾는데에 유용한 수치해석적인 방법 중의 이분법의 경우입니다. 이상!
2) 가위치법(False position)
가위치법은 이름 그대로 해석하기 어려울 수도 있는데, 영어 표현을 보시면 이해가 쉽습니다. False의 뜻인 '가짜'의 '가', position의 뜻인 '위치'가 합해져서 '가위치'라는 방법의 이름이 지정되었습니다. 즉, 근의 가짜 위치를 찾아내고 그 위치를 통해서 진짜 근을 찾아내는 수치해석적인 방법입니다.
.png)
(그래프 사진 출처 : Chapra의 응용수치해석 3판)
위 그래프를 예로 들어 설명하겠습니다. 이분법의 경우와 마찬가지로 초기값이 2개가 필요합니다. 그리고, 이 초기값(x'l과 x'u)를 통해서 x'r을 찾아내는데, 검은색 선과 같은 직선을 그어서 근의 '가짜 위치'를 지정하는 것입니다. 다시 말하면, 초기값 x'l과 x'u의 함숫값을 구하고, 이 구간 내에 근이 존재한다고 생각하게 되면, 두 함숫값의 점에 직선을 그어, 그 직선과 만나는 x축의 위치를 우선적으로 '진짜 근'이라고 가정하는 것입니다. 이렇기 때문에 x축과 만나는 점은 '가짜 위치(가짜 근)'이라는 표현을 빌려 사용하는 것입니다. 다시 말하자면,
.png)
위와 같이 대략적으로 설명드릴 수 있겠습니다. 이때, 중요한 것이 두 점사이의 직선을 긋는 것입니다. 이 직선을 매번 구해야하기 때문에 귀찮은 일이라고 생각되겠지만, 계산은 어차피 컴퓨터가 수행하는 것이므로 개념만 이해하면 됩니다. 두점 사이의 직선은
.png)
위와 같이 두 점 사이의 직선을 구할 수 있습니다. 1)번은 고등학교 때에 배웠던 두 점이 주어졌을 때에 직선을 구하는 공식입니다. 이를 가위치법에 적용하기 위해서 이 공식에 (x'r, 0)을 대입하여 주어 2)번 처럼 x'r을 구할 수 있습니다. 그리고 2)번의 표현은 가위치법에서 정식으로 표현하는 x'r을 구하는 공식입니다. 앞서 말했듯이 1)번 공식에 (x'r, 0)을 대입하고, (x1, y1)에 (x'l, f(x'l))을 대입하고, (x2, y2)에 (x'u, f(x'u))를 대입하면 2)번과 같은 공식을 만나보실 수 있습니다.
이렇게 진행한 것이 1회 반복한 것입니다. 이제 이를 통해서 다시, 2번째 가짜위치를 찾아내야 합니다. 이분법과 마찬가지로 함숫값을 서로 곱하여 0보다 작은 구간을 다시 판별하여 그 구간 내에 적어도 1개 이상의 근이 존재한다는 가정하여 가위치법을 수행하면 됩니다. 즉,
.png)
위와 같은 순서로 가위치법을 진행할 수 있습니다. 즉, 가위치법은 근의 가짜위치를 1차 직선을 그어서 찾아보고 그게 근이 아니라면, 다시 근이 존재할 것 같은 구간을 설정하여 다시 1차직선을 그어보면서 근을 찾아보는 것입니다.
이번 포스팅에서는 수치해석적으로 근을 구하는 방법인 2가지(이분법, 가위치법)를 알아보았습니다. 간략하게나마 글로 설명한다는 것이 잘 이해가 될지 모르겠지만, 순서대로 의식의 흐름?대로 설명했으니 차근차근 글자의 의미를 알아가시면서 이해하시면 충분히 이해하실 수도 있을거라 생각이 됩니다. 추가적인 질문은 댓글을 통해서 받고 있으니 궁금하신 점은 댓글을 이용해주시길 바랍니다. (단, 이러한 문제가 있는데 너무 어려워요... 풀어주세요! 이런 질문은 받지 않습니다.)
반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
| Cramer 공식, 순수 Guass 소거법, LU 분해법 예제 (2) | 2017.11.06 |
|---|---|
| 3x3 행렬식 Determinant 쉽게 구하는 방법 (6) | 2017.11.01 |
| 자주 사용하는 공학 기호 (0) | 2017.08.01 |