반응형
머릿속 도서관을 만들자.
안녕하세요. 이번에는 고등물리에서 자주 등장하는 케플러 2,3 법칙 문제를 들고와서 풀어보겠습니다. 이 글을 읽으시는 분들께 많은 도움이 되길 바랍니다. 그럼 열공하세요~^^
[문제]
그림은 xy평면에서 원점에 있는 행성을 한 초점으로 하는 타원 궤도를 따라 운동을 하는 위성 A, C와 행성을 중심으로 하는 원 궤도를 따라 운동하는 위성 B를 나타낸 것이다. P, Q는 A, C가 행성에서 가장 먼 지점이고, A의 공전 주기는 T이다.
이에 대한 설명으로 옳은 것만을 <보기>에서 있는 대로 고른 것은? (단, A, B, C에는 행성에 의한 만유인력만 작용한다.)
|
<보기>
ㄱ. 가속도의 크기는 B가 P에 있는 A의 4배이다.
ㄴ. 속력은 B가 Q에 있는 C보다 작다.
ㄷ. C의 공전 주기는 2T/3 이다.
|
[선택지]
① ㄱ ② ㄴ ③ ㄱ,ㄷ ④ ㄴ,ㄷ ⑤ ㄱ,ㄴ,ㄷ
[문제이해]
행성 1개, 위성 3개의 상황을 주어주고 케플러 법칙을 잘 이해하고 있는지 묻는 문제입니다. 간단한 문제이지만, 대략적이나마 풀이를 해보겠습니다. 그리고 A의 공전주기는 T라고 합니다.
[문제풀이]
문제에서 주어진대로, ㄱ,ㄴ,ㄷ 순서대로 풀어보겠습니다.
먼저, ㄱ부터 풀어보겠습니다.
ㄱ. 가속도의 크기는 B가 P에 있는 A의 4배이다.
행성을 중심으로 위치한 위성의 가속도의 크기는 행성으로부터 거리의 제곱에 반비례합니다. 따라서, B의 거리는 2r, A의 거리는 4r이므로, 가속도는 B가 A의 4배입니다. (거리가 2배이므로 가속도는 2의 제곱인 4배이다.) 따라서 ㄱ은 맞는 말입니다.
다음으로, ㄴ을 풀어보겠습니다.
ㄴ. 속력은 B가 Q에 있는 C보다 작다.
그림을 보시면 B는 원운동하고 있어서 가속도나 속력은 일정합니다. 그리고 위성 C는 Q점에 위치할 때가 원일점 상태입니다. 이때 Q점에 있는 C 위성은 B보다 행성에서 멀리있으므로 B보다 느려야 정상입니다. (만유인력의 크기는 거리에 반비례합니다.) 따라서 ㄴ은 틀린 말입니다.
마지막으로, ㄷ을 풀어보겠습니다.
ㄷ. C의 공전 주기는 2T/3 이다.
케플러 제 3법칙에 대해 알고 있어야합니다. 3법칙은 조화 법칙으로 공전 주기의 제곱은 궤도의 장반경의 세제곱에 비례합니다. 따라서 아래와 같이 풀이할 수 있습니다.
따라서, 위성 C의 주기는 위와 같아서 ㄷ은 틀린 말입니다.
이때, 각 위성의 장반경을 구하는 방법은 [장반경 = (근일점 반경 + 원일점 반경) /2] 입니다.
[개념]
- 케플러 제 2법칙
- = 면적 속도 일정 법칙
- 태양과 행성을 잇는 직선은 같은 시간 동안 같은 면적을 휩쓸고 지나간다.
- 제플러 제 3법칙
- = 조화 법칙
- 행성의 공전 주기의 제곱은 행성의 타원 궤도 긴반지름의 세제곱에 비례한다.
[정답]
① ㄱ
반응형
LIST
'공학 문제해결 > 물리' 카테고리의 다른 글
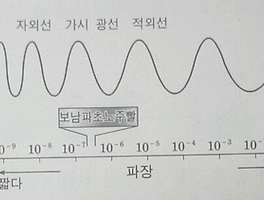
| 【물리】 전자기파 문제풀이 (0) | 2018.03.27 |
|---|---|
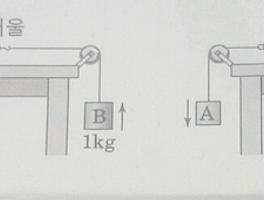
| 【물리】 등가속도 운동 및 용수철 저울 문제풀이 (0) | 2018.03.24 |
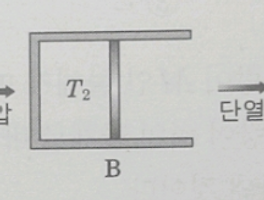
| 【물리】 등압, 단열과정 열역학 문제풀이 (0) | 2018.03.15 |