양단고정보 축방향응력 문제 풀이

안녕하세요. 이번 포스팅에서는 다음 그림과 같이 생긴 양단고정보 내에 힘이 작용할 때에 어떻게 해석해야하는지 풀어보는 문제입니다. 간단하면서도 햇갈리기 쉬운 양단고정 상태이기 때문에 천천히 읽으시면서 이해하시면 좋을 것 같습니다.

[문제]

- 실제로 공기업 필기시험에 기출된 문제 입니다.

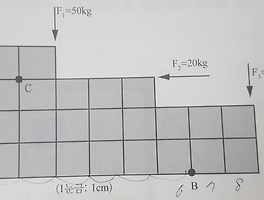
Q. 다음의 양단고정보에서 하중이 B점에 작용할 때 부재 BC의 축방향응력의 크기는?

(단, AB부재 단면적은 2A이고, BC부재의 단면적은 A이며, 탄성계수는 서로 동일하다.)

[그림]

[답] P/5A 

[문제설명]

보의 총 길이가 L이고 좌측에 AB부재 부분의 길이는 L/3이며 면적은 2A이고, 우측의 BC 부재의 길이는 2L/3, 면적은 A일 때, B지점에 힘 P가 작용합니다. 이때의 각 부재에 걸리는 내부 응력은 얼마인지 묻고 있습니다. 좌우측이 고정되어 있는 고정단이기 때문에, 반력이 2개가 생기고 면적이 다르기 때문에 내부 응력의 크기도 달라질 것입니다. 우선 문제에서는 부재 BC에 걸리는 응력만 묻고 있습니다.

[문제풀이]

우선 각 AB, BC 부재의 조건을 정리해봅시다.

1) AB 부재 : 단면적 2A, 길이 L/3

2) BC 부재 : 단면적 A, 길이 2L/3

그리고 위 그림에 제가 손글씨로 표현한 것처럼, 좌우에 고정단이므로 반력 R'A, R'C가 작용한다고 하겠습니다. 기호 R은 reaction의 약자고 A와 C는 각 지점과 가깝기때문에 그렇게 하첨차로 표시하였습니다. 이제 여기서 힘 평형 방정식을 세웁니다.

위 힘평형 방정식은 왼쪽 방향을 (-) 부호로, 오른쪽 방향을 (+) 부호로 가정한 것입니다. 그렇게 축방향(x축 방향)의 합력은 0이다라는 방정식을 통해 위 수식을 도출합니다.

그리고  이 공식을 기억하시나요? Hooke's Law에서 나온 공식입니다. 위 그림에서 양 부재의 변화량의 합도 0이 되어야 합니다. (미지수가 양쪽 고정단의 반력 2개 이므로 방정식도 2개가 필요합니다.) 이 수식을 아래와 같이 양 부재의 변위의 크기가 같다는 식으로 풀 수 있습니다.

즉, R'A는 R'C의 4배라는 것을 알 수 있습니다. 그리고 이 결과를 다시 위에서 구했던 힘 평형방정식의 결과 수식에 대입합니다.

대입하게되면 위와 같이 양쪽 고정단에서 나타나는 반력들의 크기가 주어진 힘 P를 통해 나타내집니다. 이것이 답으로가는 마지막 계산이었고, 문제에서는 부재 BC에서의 응력을 묻고 있으니, 위에서 구한 부재 BC에 걸리는 힘인 반력 R'C의 값으로 응력을 구해줍니다.

따라서, 부재 BC에 걸리는 응력(시그마'BC)는 P/5A가 정답이 됩니다. 이상!