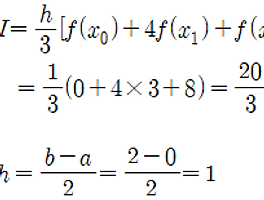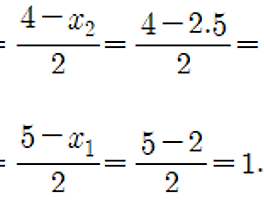반응형
"진심은 누구에게나 통하는 법이에요.
만약 그 진심을 가볍게 생각하는 사람이라면
당신은 그 사람에게 과분한 사람이에요."
안녕하세요. 이번 포스팅에서는 수치해석에서 'Newton 2차 보간다항식'을 이용하여 예제를 풀어보겠습니다. 수치해석의 일종의 방법으로써 긍정적인 해답을 찾기위한 것입니다. 아래의 쉬운 예제를 통해 알아가실 수 있으면 좋겠습니다. 기타 질문사항은 댓글을 남겨주시길 바랍니다. (너무 어려운건 글로 표현하기 힘들어요....ㅠㅜㅎㅎ)
[문제]
아래의 조건을 통하여 x = 1일 때의 함수값을 구하여라.
<조건들>
위의 점 3개로 이번 포스팅의 예제를 풀어보겠습니다. 위 3개의 조건들을 통하여 Newton 2차 보간 다항식을 적용하여 f(1)의 값을 도출해보겠습니다.
Newton 2차 보간다항식 기본 개념 및 공식
우선, 뉴턴 2차 보간다항식은 위와 같은 공식이 적용됩니다. 이 방법을 적용하기 위해서는 우선, 위 공식이 만들어진 것에 대한 이해가 필요합니다. 우선 제일 위에 적혀있는 f2(x)는 '2차' 방정식에서 기본으로 적용되는 '틀'입니다. 그리고 1)~3)에서 각 x1, x2, x3를 대입하면서 나오게되는 b1, b2, b3의 값들입니다. 이들은 결국 계산하게되면, 전부다 일정한 상수값을 가지게 됩니다. 위 식을 이해를 통하여 암기하신 다음에 다음과 같이 풀이를 진행할 수 있습니다.
[문제풀이]
위에 나열된 공식에서 1)번부터 차례로 주어진 조건들을 대입해줍니다.
즉, b1 = 8, b2 = -2, b3 = 1 을 얻게됩니다. 이제 이들을 제일 처음 뉴턴 2차 보간다항식에 대입합니다. 이때, 대괄호로 표현된 f[~]의 표시는 수학적 표현방법의 일종입니다. 이런식으로 간단하게 표현한다 정도만 이해하시면 됩니다. 논문이나 과제 등을 작성하실 때에는 같이 적어주시면 좋은 수학적 표현법입니다.
최종적으로 뉴턴 2차 보간다항식을 위와 같이 얻을 수 있습니다.
그리고 마지막으로 문제에서 원하는 x = 1일때의 함숫값을 구해보겠습니다. 위 조건들을 통해 구한 함수가 위와 같이 f2(x)와 같이 나타내었습니다. 이를 구하는데 적용된 x의 범위가 0에서 4이므로, 그 사이에 있는 x = 1에서는 충분히 근접하다고 어느정도 고려할 수 있습니다. 문제에서는 위 3개의 점 조건으로만 구하라고 하였으므로, 그대로 대입해주면 됩니다. 즉,
가 되어, 최종적으로 문제에서 구하고자하는 f(1)의 값은 5가 됩니다. 이상!
반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
| 【수치해석】 Simpson 1/3 공식 예제 풀이 (0) | 2017.12.20 |
|---|---|
| 【수치해석】 Gauss-Seidel법, Jacobi 반복법 예제 풀이 (7) | 2017.12.20 |
| Cramer 공식, 순수 Guass 소거법, LU 분해법 예제 (2) | 2017.11.06 |