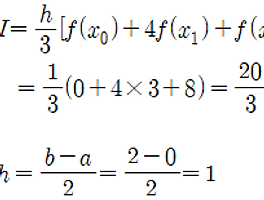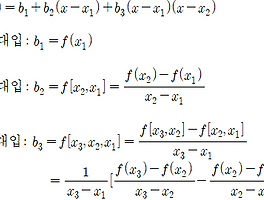반응형
"If I'd had some set idea of a finish line, don't you think I would have crossed it years ago?"
"결승선에 대한 어떤 정해진 생각이 있었다면 내가 그 결승선을 이미 몇 년 전에 넘었을 거라고 생각하지 않으세요?"
- 빌 게이츠
안녕하세요. 이번 포스팅에서는 '통계용어' 중에서 기본적인 개념들만을 모아서 정리해 보았습니다. 참고하시어 도움이 되시길 바랍니다.
-
변량 : 자료를 수량으로 나타낸 것
- 계급 : 변량을 일정한 간격으로 나눈 구간
- 계급의 크기 : 구간의 너비
- 도수 : 각 계급에 속하는 자료의 개수
- 계급값 : 각 계급의 가운데 값
- 5개 숫자요약 (five - number summary) : 자료를 요약하는데 사용되는 5개 요약자료로 최소값, 1사분위수, 중앙값, 3사분위수, 최대값이다.
- 추정 (estimation) : 추정이란 표본을 이용하여 모집단의 미지의 수를 얻는 것을 말한다.
- 모집단 (population) : 관심 대상의 모든 원소의 집합
- 모수 (parameter) : 모집단의 통계값
- 표본 (sample) : 모집단에서 추출된 부분집합
- 표본공간 : 일어날 수 있는 모든 결과의 집합
- 표본통계량 (sample static) : 표본을 요약하는데 사용되는 통계량 (표본평균, 표본분산, 표본표준편차 등)
- 통계량 (statistic) : 표본의 통계값
- 구간추정치 (interval estimate) : 모수 값이 포함되어 있다고 믿어지는 구간
- 가중평균 (weighted mean) : 자료값에 자료의 중요도를 반영하는 가중치를 부여하여 계산하는 평균
- 표본평균 (sample mean) : 변수의 총합을 그 항의 개수로 나눈 값
- 평균의 표집분포 (sampling distribution of mean) : 같은 모집단에서 n크기의 표본을 무한 반복하여 뽑아서 추정한 표본 평균값의 분포
- 산포도 (scatter diagram) : 두 개의 정량적 변수의 관계를 보여주는 그래프적 방법
- 추세선 (trendline) : 두 변수의 근사적 관계를 보여주는 직선
- 중앙값 (median) : 자료를 오름차순으로 정렬할 때 중앙에 위치한 자료값으로 중심위치를 측정하는 방법
- p분위수 (percentile) : 그 값보다 같거나 작은 비율이 적어도 p퍼센트이며 같거나 큰 비율이 적어도 (1-p) 퍼센트인 자료값. 50분위수는 중앙값이다.
- 사분위수 (quartiles) : 25분위수, 50분위수, 75분위수를 말한다. 이들은 1사분위수, 2사분위수, 3사분위수로 부른다. 사분위수는 분포를 4등분하고 각 등분은 자료의 약 25%를 포함한다.
- 범위 (range) : 변동성의 척도로 (최대값 - 최소값)으로 정의된다..
- 최빈수 (mode) : 도수분포에서 도수가 가장 많이 발생하는 값
- 분산 (variance) : 변수의 값과 그 값의 평균값에 대한 편차의 제곱값을 더하여 얻은 값을 n-1로 나누어 준 값. 이 값은 평균을 중심으로 자료가 어떤 분포를 하는지를 나타내는데 이 값이 작으면 관측치들이 평균 주위에 많이 분포되어 있다는 것을 나타내고 이 값이 클수록 관측치가 평균으로부터 떨어져 있다는 것을 나타낸다.
- 표준편차 (standard deviation) : 분산에 제곱근을 탠하여 그 중에서 양(+)의 값
- 변동계수 (분산계수, coefficient of variation) : 표준편차의 평균에 대한 백분율. 일반적으로 평균이 증가함에 따라 표준편차가 증가하므로 평균을 무시하고 표준편차만을 가지고 분산도를 비교하는 것보다 표준편차의 평균ㄴ에 대한 백분율을 구해 비교해보는게 바람직하다.
- 편도 (비대칭도, 왜도, skewness) : 분포의 비대칭의 정도. 자료의 분포형태를 측정하는 방법으로 왼쪽으로 치우치면 음수, 대칭이면 0, 오른쪽으로 치우치면 양수가 된다.
- 공분산 (covariance) : 두 확률변수 X와 Y의 선형관계를 나타낸다.
- 표준오차 (standard error) : 표본평균이 모평균과 얼마나 퍼져 있는지를 나타내는 표준편차 추정치
- 확률변수 (random variable) : 실험의 결과를 숫자로 표현
- 확률분포 (probability distribution) : 확률이 확률변수값에 따라 어떻게 분포하는가를 나타내는 것
- 정규분포 (normal distribution) : 정규분포는 연속적이고 좌우대칭인 종모양의 확률분포로서 우리가 관측하는 자료들은 일반적으로 정규분포와 비슷한 형태를 가지고 있다.
- 표준정규분포 (standard normal distribution) : 정규분포의 성질을 이용하여 확률계산을 할 목적으로 임의의 정규분포를 변환시켜 만든 것
- 확률밀도함수 (probability density function) : 연속확률변수의 확률을 계산하는데 사용되는 함수. 어떤 구간에 해당하는 확률은 확률밀도함수 그래프 아래의 면적이다.
반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
| 【수학】검산, 구거법이란? (2) | 2018.04.06 |
|---|---|
| 【수치해석】 Simpson 1/3 공식 예제 풀이 (0) | 2017.12.20 |
| 【수치해석】 Newton 2차 보간다항식 예제 풀이 (0) | 2017.12.20 |