반응형
"지나치게 도덕적인 사람이 되지 마라. 인생을 즐길 수 없게 된다. 도덕 그 이상을 목표로 하라. 단순한 선함이 아니라 목적이 있는 선함을 가져라."
- 헨리 데이비스 소로우
안녕하세요. 이번 포스팅에서는 유체역학 문제 중, 수위가 다른 양쪽 사이에 수직벽이 있고, 그 사이에 있는 오리피스를 통해 액체가 지나갈 때의 속도를 구하는 문제입니다. 주로 한쪽에만 있는 것만을 풀어보셨을텐데, 이번 문제도 그러한 문제들과 아주 유사하게 풀 수 있습니다. 다만, 공학적 개념이 부족하다면 처음 문제를 접하면 어려워하실 수도 있을 것 같아서 이렇게 포스팅하게 되었습니다. 이 글을 읽으시는 분들께 많은 도움이 되길 바랍니다.
[문제]
그림과 같이 수직벽의 양쪽에 수위가 다른 물이 있다. 벽면에 붙인 오리피스를 통하여 수위가 높은 쪽에서 낮은 쪽으로 물이 유출되고 있다. 오리피스에서의 속도는 얼마인가?
[문제이해]
그림을 보시면 중앙에 수직벽이 있고, 좌우측에 물(액체)이 차있습니다. 이때, 양쪽의 수위가 다른 것을 확인할 수 있고, 중앙에 있는 수직벽에는 오리피스 형태로 구멍이 나있는 것을 알 수 있습니다. 그러면 당연히 수위차가 발생했기 때문에 압력차 등으로인해 오리피스를 통해 물이 지나갈 것이라는 것도 알 수 있습니다. 또한, 좌측의 물의 수위가 더 높기때문에 물은 좌 → 우로 흐를 것이라는 것도 알 수 있습니다.
(이때, 양 수위 기준면에 아래방향 삼각형의 의미는 표시된 곳이 수면이라는 뜻입니다. 즉, 역삼각형이 표시된 기준선 아래는 '물'이 가득차 있다는 말입니다.)
[문제풀이]
그럼 이제 문제를 풀어보겠습니다. 우선, 그림에서 주어진 상태에서 오리피스 중앙에서 각 최대 수위까지의 거리를 Z1, Z2로 주어졌으므로, 이 선을 기준으로하여 문제를 풀어보겠습니다. 이렇게 문제가 주어지면 '베르누이 방정식'을 아래와 같이 적용하면 쉽게 문제를 풀 수 있습니다.
베르누이 방정식은 위와 같이 정의되고, 문제에서 오리피스 중앙을 통과하는 수평선을 기준으로 하면, Z1 = Z2 = 0 이 됩니다. 그리고 좌측에서의 속도(v1)도 0이 됩니다. 문제에서 구하고자하는 속도는 우측의 속도 즉, v2가 됩니다. 또한, 압력(P1, P2)은 비중 x 깊이가 되어 아래와 같이 베르누이 방정식을 적용할 수 있습니다.
이해가 되시나요? 앞서 말했듯이, 베르누이 방정식에 Z1 = 0, Z2 = 0, v1 = 0을 대입하고, 압력은 P1 = γZ1, P2 = γZ2 를 (압력 = 비중 x 깊이) 대입한 것입니다. 즉, 답은 아래와 같고, 최종적으로보면 양 수위차에 대하여 속도값이 정의된다는 것을 알 수 있습니다.
[답]
이상!
【유체역학】 물에 잠긴 평판에 작용하는 힘(전압력) 구하기
【유체역학】 Pressure(압력) 관련 단위 [ksi, psi] 변환 알아보기
【유체역학】 물에 잠긴 물체의 전압력이 작용하는 수직거리 구하는 공식
【유체역학】 모세관 현상의 원리 + 높이 구하는 방법(공식)
반응형
LIST
'공학 문제해결 > 유체역학' 카테고리의 다른 글
| 【유체역학】 풍동 모형실험 레이놀즈 상사성 문제풀이 (0) | 2018.04.18 |
|---|---|
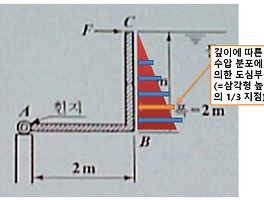
| 【유체역학】 전압력이 작용하는 수문 힌지 문제 풀이 (2) | 2017.08.06 |
| 【유체역학】 물에 잠긴 평판에 작용하는 힘(전압력) 구하기 (4) | 2017.07.27 |