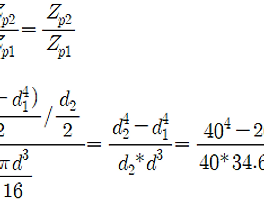반응형
"Time is the coin of your life. It is the only coin you have, and only you can determine how it will be spent. Be carefullest you let other people spend it for you."
"시간은 인생의 동전이다. 시간은 네가 가진 유일한 동전이고, 그 동전을 어디에 쓸지는 너만이 결정할 수 있다. 네 대신 타인이 그 동전을 써버리지 않도록 주의하라."
- 칼 샌드버그
안녕하세요. 이번 포스팅에서는 재료역학에서 압축하중이 작용하는 원형봉 부재의 푸아송 비를 구하는 간단한 문제입니다. 푸아송 비에 대한 개념 이해를 위한 간단한 문제로 이해해주시면 좋을 것 같습니다.
[문제]
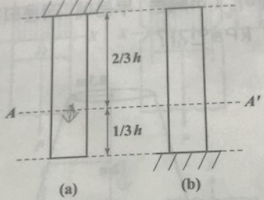
그림과 같은 원통형 부재에 P = 10 ton의 하중이 작용하여 하중작용 방향으로 0.03cm 줄었고, 하중작용 직각방향으로 0.0015cm 가 늘어났다면 이 부재의 푸아송 비는?
[문제풀이]
우선, 푸아송 비에 대한 개념과 공식을 이해해보겠습니다.
- 푸아송비 (Poisson's ratio) : 재료 내부에 생기는 수직 응력에 의한 가로 변형과 세로 변형의 비. 탄성 한도 내에서는 동일 재료에 대하여 일정하다. - 도해 기계용어사전
- 관련 공식
(이때, ν는 푸아송비이고, m은 푸아송(상)수입니다.)
개념과 공식은 위와 같고, 문제에서 주어진 조건들을 위 식에 대입하기 위해 이해해보겠습니다. 우선, 문제에서 압축하중이 축방향으로 작용하고 있습니다. '하중작용 방향으로 0.03cm 줄었고'라는 말은 축방향으로의 변형량(δ)이 0.03cm라는 뜻이고, '하중작용 직각방향으로 0.0015cm가 늘어났다면'라는 말은 직경방향으로의 변형량(d')가 0.0015cm라는 뜻입니다. 즉,
이라고 문제에서 주어져있습니다. 이렇게 이해한 것을 이제, 위의 푸아송비의 공식에 대입합니다. 직경과 길이는 문제의 그림에 나와있는 그대로를 대입하겠습니다.
단위는 전부 cm이므로 일부러 바꾸지 않았습니다. 푸아송비는 무차원 단위이기 때문에 분자/분모의 단위가 같다면 어차피 상쇄되기 때문입니다. 즉, 위와 같이 원통봉의 푸아송비를 구할 수 있었습니다. 이상! 궁금하신 점은 댓글을 통해 블로거와 소통하실 수 있습니다!
반응형
LIST
'공학 문제해결 > 재료역학' 카테고리의 다른 글
| 【재료역학】 직렬병렬 스프링 처짐량 문제풀이 (0) | 2018.04.23 |
|---|---|
| 【재료역학】 자중 비교 문제풀이 (2) | 2018.04.12 |
| 【재료역학】 동일 단면적 중실축, 중공축의 비틀림 비교 문제풀이 (8) | 2018.04.12 |