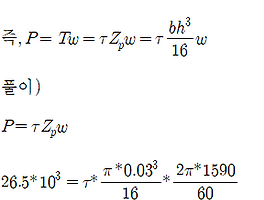반응형
"Gravitation cannot be held responsible for people falling in love."
"만유인력은 사랑에 빠진 사람을 책임지지 않는다."
- 알버트 아인슈타인
안녕하세요. 이번 포스팅에서는 재료역학에서 비균일 사각단면에서의 응력을 구하는 문제를 풀어보겠습니다. 자세한건 아래 그림을 보시면 이해하시기 편할 것 같습니다. 천장에 매달린 사각봉이 일정한 단면이 아니라, 중간에 단면이 감소되었다가 다시 증가된 형태입니다. 이러한 문제는 재료역학에서 배우는 '기둥' 단원에서 배우는 것과 동일하게 문제를 풀 수 있습니다. 문제에서 중력을 언급하지 않았기 때문에 무시되므로 아래 그림을 정 반대로 바닥에 세운 기둥이라 생각하셔도 무방합니다. 아래 문제풀이에서 중력을 고려하게 된다면, 조금 달라지게 될 것입니다.
[문제]
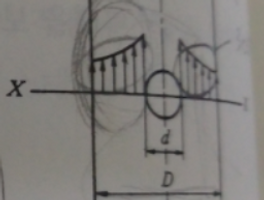
그림과 같은 지사각형의 한 변 a = 10 cm 의 단면의 일부분이 단면적 a/2 * a 로 감소되어 있을 때, 축 방향에 40 kN에 의하여 m-n 단면에 발생하는 응력은 몇 MPa인가?
[문제이해]
앞서 말했듯이, 이번 문제는 천장에 매달려있는 사각봉이지만, 중력을 고려하지 않기 때문에 바닥에 세운 기둥으로 간주하여 문제를 풀어도 무방합니다. (만약 중력을 고려하게 된다면, 천장에 매달려있고 힘 40kN과 더불어 밀도, 비중 등에 의한 무게가 발생하게 되어 이것도 신경써줘야 합니다.) 그래서 아래와 같이 간단하게 문제를 풀 수 있습니다.
위 그림에서 우측에 사각형이 그려진 것은 아마 배면도(물체를 아래에서 본 도면)로 보시면 좋을 것 같습니다. 그렇게해도 중앙에 그은 선이 숨은선으로 그려져야한다는 주의할 점이 있지만, 이번 문제는 기계제도 문제가 아니라 재료역학 문제이기 때문에 크게 신경쓰지 않겠습니다. (갑자기 프로불편러가 된 듯한 느낌?...) 그리고 문제에서 주어진 조건을 요약하면 다음과 같습니다.
① 한 변의 길이 = a = 10 cm
② 축방향 힘 = P = 40 kN
[문제풀이]
위 문제는 '기둥'으로 간주하여 문제를 풀 수 있다고 말씀드렸습니다. 그래서 아래 풀이와 같이 응력은 총 2가지가 생깁니다. 첫번째로 힘 P가 기둥을 인장시키고 있기 때문에 '인장응력'이 발생하게 되고, 사각봉의 단면이 비균일하기 때문에 중앙 측에 발생하는 '굽힘응력'이 생기게 됩니다. 즉, m-n 단면에 작용하는 응력은 '인장응력'과 '굽힘응력'으로 총 2가지 입니다.
그리고 둘 사이의 관계는 (+)와 (-) 중에서 (+)가 됩니다. 왜냐, 위 그림에서도 알 수 있듯이 단면이 우측에만 존재하고 좌측은 제거되었다고 생각할 수 있는데, 이때 굽힘은 제거된 쪽으로 굽힘이 발생하기 때문에 우측에 줄어든 단면에 대해서는 인장응력과 같은 방향으로 굽힘응력이 작용하게 됩니다. 따라서, 위와 같이 2개의 응력을 더하여 최종 응력을 구하는 개념이 됩니다.
(만약, 위 그림과는 반대로 좌측 단면이 있고, 우측 단면이 잘려진 형태라고 해도 인장응력과 굽힘응력을 더하는 개념은 동일합니다. 추가적으로, 위 문제에서 인장하중이 아니라 압축하중이 걸리게되면, 두 응력(인장, 굽힘응력)은 서로 빼주는 개념이 됩니다.)
그리고 굽힘응력은 위와 같이 σ = M / Z 로 나타낼 수 있습니다. 이때, Z는 단면계수로써 이번 문제에서는 사각단면이기 때문에 Z = bh^2/6 입니다.
이제 이렇게 구한 단면계수를 위에서 구했던 전체 응력에 대입하고, 문제에서 주어진 조건들을 아래와 같이 대입하면 됩니다.
이때, 굽힘응력에서 모멘트 M은 힘 P와 사각단면 중심까지의 거리를 곱해서 대입하게 됩니다. 이렇게 위와 같이 m-n 단면에 작용하는 전체 응력을 구해보았습니다. 언제나 궁금한 점은 댓글을 남겨주시길 바랍니다. 이상!
【재료역학】좌굴 하중(응력, 강도) 계산 오일러 공식 + 단말 계수
반응형
LIST
'공학 문제해결 > 재료역학' 카테고리의 다른 글
| 【재료역학】응력집중계수, 안전율 고려하여 두께 구하는 문제풀이 (0) | 2018.04.11 |
|---|---|
| 【재료역학】 단순보 비균일 분포하중 문제풀이 (3) | 2018.04.02 |
| 【재료역학】 집중하중 외팔보의 처짐 및 처짐각 (0) | 2018.03.31 |