반응형
[연습문제 2.5]
다음 식은 x의 함수로서 y값을 계산하는 데 사용된다.
여기서 a와 b는 매개변수이다. MATLAB을 실행할 수 있는 식을 써라. 여기서 a=2, b=5 그리고 x는 증분  로 0에서 pi/2까지의 값을 가지는 벡터이다. 식이 최소 개수의 구두점들(점 표기)을 사용하여 y에 대한 벡터를 산출할 수 있도록 하라. 또한 벡터
로 0에서 pi/2까지의 값을 가지는 벡터이다. 식이 최소 개수의 구두점들(점 표기)을 사용하여 y에 대한 벡터를 산출할 수 있도록 하라. 또한 벡터  을 계산하라. 여기서 z의 각 원소는 y의 각 원소의 제곱이다. x, y와 z를 합하여 행렬 w로 만들라. 여기서 행렬 w는 각 열은 x, y와 z변수들 중 한개를 나타내게 하고, short g 포맷을 사용하여 w를 출력하라. 또한 x에 대한 y와 z의 그래프를 라벨을 포함시켜 그려라. 그래프에 설명문(legend)을 포함하라(설명문을 포함시키는 방법을 알기 위해서는 help를 사용하라). y에 대해서는 1.5 point의 붉은색의 점선과 14 point의 붉은색 변, 흰색 면의 별 모양(pentagram) 기호를 사용하라. z에 대하여는 표준 크기의(즉 기본값) 파란색 실선과 표준 크기의 파란색 변과 녹색 면의 사각형 기호를 사용하라.
을 계산하라. 여기서 z의 각 원소는 y의 각 원소의 제곱이다. x, y와 z를 합하여 행렬 w로 만들라. 여기서 행렬 w는 각 열은 x, y와 z변수들 중 한개를 나타내게 하고, short g 포맷을 사용하여 w를 출력하라. 또한 x에 대한 y와 z의 그래프를 라벨을 포함시켜 그려라. 그래프에 설명문(legend)을 포함하라(설명문을 포함시키는 방법을 알기 위해서는 help를 사용하라). y에 대해서는 1.5 point의 붉은색의 점선과 14 point의 붉은색 변, 흰색 면의 별 모양(pentagram) 기호를 사용하라. z에 대하여는 표준 크기의(즉 기본값) 파란색 실선과 표준 크기의 파란색 변과 녹색 면의 사각형 기호를 사용하라.
[문제풀이]
우선, 문제 자체가 너무 길고 묻고 있는 것이 한두개가 아니라서 천천히 순차적으로 풀어보겠습니다. 각 풀이에 이해를 돕기 위해 가장 윗부분에 문제의 해당하는 문장을 '작은따옴표'로 적어놨으니 아래를 보시면서 matlab이 구현되는 것도 같이 보시면 좋을 것 같습니다.
'MATLAB을 실행할 수 있는 식을 써라.'
exp와 sin에 x가 포함되므로 함수 밖에 제일마지막에 콤마(.)를 붙여주고 뒤에 있는 다항식에도 마찬가지로 x 바로 뒤에 콤마(.)를 붙여줘서 x가 행렬이기 때문에 요소별로 계산하라는 명령을 넣어주어 수식을 만들어줍니다. 이 식을 적는 것을 이해하는게 이번 문제의 대부분인 듯 합니다. 일반적인 수식과 matlab에서 이해하는 수식의 표현이 조금 다른데, 그 차이만 이해하면 충분하다고 생각됩니다.
'여기서 a=2, b=5 그리고 x는 증분  로 0에서 pi/2까지의 값을 가지는 벡터이다. 식이 최소 개수의 구두점들(점 표기)을 사용하여 y에 대한 벡터를 산출할 수 있도록 하라.'
로 0에서 pi/2까지의 값을 가지는 벡터이다. 식이 최소 개수의 구두점들(점 표기)을 사용하여 y에 대한 벡터를 산출할 수 있도록 하라.'
위가 a, b, x를 입력한 것입니다. a=2뒤에 세미콜론(;)을 넣어준 것은 결과값을 바로 보여주지 않아도 된다고 적은 것입니다. 뒤에 세미콜론을 붙이지 않으면 위의 x값과 같이 enter하게되면 바로 아래에 x의 값을 나타내어 주게 되어있습니다.
이전에 matlab에서 이해할 수 있는 표현으로 적은 함수 y를 입력하니 위와 같이 답이 행렬로 나왔습니다. 이는 a와 b는 1x1 행렬인 스칼라이지만, x값이 행벡터이기 때문에 y값도 행벡터로 나오게 된 것입니다.
'또한 벡터  을 계산하라. 여기서 z의 각 원소는 y의 각 원소의 제곱이다.'
을 계산하라. 여기서 z의 각 원소는 y의 각 원소의 제곱이다.'
y의 각요소별로 제곱한 값을 z에 대입했습니다. 이때, 행렬의 각 요소별로 연산되는 것은 뒤메 콤마(.)를 붙여주면 됩니다.
'x, y와 z를 합하여 행렬 w로 만들라. 여기서 행렬 w는 각 열은 x, y와 z변수들 중 한개를 나타내게 하고, short g 포맷을 사용하여 w를 출력하라.'
short g 는 무시했습니다. 새로운 행렬 w를 x와 y, z를 통해 만드는 과정입니다. w = [x;y;z]처럼 행렬을 만들 수 있습니다. 이때, 열구분은 띄어쓰기로 하지만 행구분은 세미콜론으로 해주면 됩니다.
'또한 x에 대한 y와 z의 그래프를 라벨을 포함시켜 그려라. 그래프에 설명문(legend)을 포함하라(설명문을 포함시키는 방법을 알기 위해서는 help를 사용하라).'
설명문은 무시했습니다. 명령어 plot (x,y)를 통해 위 그래프가 나왔습니다. 라벨도 포함시켜주면 되는데 위 이미지에서는 title이라는 명령어를 통해 'x에 대한 y'라는 제목만 붙여주었습니다. x축에 대한 라벨을 붙여주려면 xlabel을 통해서 가능합니다. 마찬가지로 y축은 ylabel을 통해서 y축에 대한 라벨을 붙여줄 수 있습니다.
plot (x,z)를 통해 위 그래프가 나왔습니다.
'y에 대해서는 1.5 point의 붉은색의 점선과 14 point의 붉은색 변, 흰색 면의 별 모양(pentagram) 기호를 사용하라.'
말뜻을 제가 제대로 이해해서 적었는지 모르겠네요. 여튼 명령어와 그래프는 위와 같이 그렸습니다. 그래프는 plot이라는 명령어를 통해서 나타내고 plot(x,y,'~~')에서 가장 뒤에 필요한 값을 표현해줄 수 있습니다. 선의 두께는 LineWidth, 마크의 크기는 MarkerSize, 마크의 선색은 MarkerEdgeColor, 마크의 면색은 MarkerFaceColor로 구현할 수 있습니다. 아래도 같은 방법으로 그래프를 그릴 수 있습니다.
'z에 대하여는 표준 크기의(즉 기본값) 파란색 실선과 표준 크기의 파란색 변과 녹색 면의 사각형 기호를 사용하라.'
위와 같이 그릴 수 있었습니다. 이상!
여러분들의 소중한 공감♥ 클릭이 블로거에겐 큰 힘!이 됩니다^^
로그인하지 않아도 가능합니다!
[프로그램/MATLAB] - 【MATLAB】 기초 연산 문제 풀이
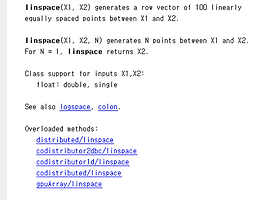
[프로그램/MATLAB] - 【MATLAB】 기초 연습문제 2.1~2.3 : 콜론 표기법과 linspace
[프로그램/MATLAB] - 【MATLAB】 완전 기본 명령어 20가지
반응형
LIST
'프로그램 > MATLAB' 카테고리의 다른 글
| 【MATLAB】 표준정규확률 밀도함수 그래프 문제풀이 (0) | 2017.09.20 |
|---|---|
| 【MATLAB】 기초 연산 문제 풀이 (0) | 2017.09.16 |
| 【MATLAB】 기초 연습문제 2.1~2.3 : 콜론 표기법과 linspace (4) | 2017.09.16 |