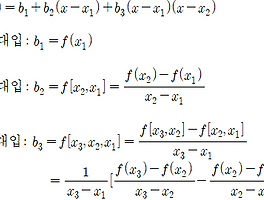반응형
이번 문제는 수치해석에서 사용하는 Cramer, 순수 Guass 소거법, LU 분해법을 통해서 선형방정식의 근을 찾는 문제입니다. 선형방정식 3개, 근 3개짜리의 문제를 가지고 와서 예제처럼 풀어볼 것입니다. 최종적으로 보시면 각 방법을 통해서 구한 근이 모두 동일하다는 것을 알 수 있습니다.
[문제]
Q. 다음과 같은 방정식을 Cramer 공식, 순수 Guass 소거법, LU 분해법으로 근을 구하시오.
1) Cramer 공식을 통해 근을 구하시오.
2) 순수 Guass 소거법을 통해 근을 구하시오.
3) LU 분해법으로 근을 구하시오.
[방정식]
.png)
[답] x1 = 1, x2 = 2, x3 = 3
[문제설명]
3개의 방정식이 있고, 이 것의 근을 구하는 방법인 3가지의 방식을 통해서 근을 구하라는 문제입니다. 방정식이 선형이므로 문제에서 주어진 3가지의 방식을 모두 만족합니다. 그래서 아래와 같이 순차적으로 문제를 풀 수 있습니다.
[문제풀이]
우선, 문제에서 주어진 3개의 방정식을 크래머, 가우스, LU 방법을 사용하기 위해 행렬으로 표현해줍니다.
.png)
행렬은 '[ ]' 표시를 하고, 열벡터는 '{ }' 표시를 하였습니다. 나중에 나오겠지만 행렬식은 '| |' 표시를 하겠습니다. 그러면 가장 좌측의 3x3 행렬이 계수행렬 [A]가 됩니다. 각각을 아래와 같이 정의하겠습니다.
.png)
이제 문제에서 주어진 3가지 방법으로 각각 풀어보겠습니다.
1) Cramer (크래머) 공식을 사용하여 근 구하기
.png)
D라는 말은 각 행렬의 행렬식(Determinant)의 앞자리인 D를 따와서 표현한 것 입니다. 그래서 계수행렬 [A]의 행렬식인 |D| 를 구해주고, D1, D2, D3는 우항에 있는 {b} 행렬을 각 1,2,3번째 열에 대신 넣어줌으로써 구한 행렬식을 통해서 나타냅니다. 그리고 마지막 줄에 있는 것처럼 x1 = D1/D 와 같이 각각의 근을 구할 수 있습니다. 3x3 행렬의 행렬식을 위와 같이 손쉽게 구하는 방법은 아래의 링크를 참고해주세요.
2) 순수 Guass 소거법을 사용하여 근 구하기
순수 가우스 소거법은 피봇팅을 하면 안됩니다. 피봇팅이란 각 방정식의 행위치를 바꾸는 것인데요. 이번 문제에서는 '순수'하게 풀어야 하므로 개념을 적용하지는 않겠습니다.
.png)
우선은 순수 가우스 소거법을 위 방정식에 적용해줍니다. 그러면 위와 같은 순서대로 작업이 진행됩니다. 계수행렬을 상삼각행렬(Upper triangular matrix)으로 만들어주는 과정입니다. 그래서 위 수식에서 마지막 줄에있는 계수행렬이 상삼각행렬이 됩니다. 이때, 상삼각행렬은 주대각선을 기준으로 아래의 원소가 전부 '0'인 것을 말합니다.
참고)
- 상삼각행렬 (upper triangular matrix) : 주대각선 아래 방향의 원소들의 값이 모두 '0'이고 위 방향의 원소는 값을 가지고 있는 행렬
- 하삼각행렬 (lower triangular matrix) : 주대각선 위 방향의 원소들의 값이 모두 '0'이고 아래 방향의 원소들은 값을 가지고 있는 행렬
.png)
이제 위와 같이 상삼각행렬의 제일 아래 행부터 계산에 들어가면 각각의 근을 구할 수 있습니다. (직접 말로 설명해서 헷갈리는 것보다 위에 적은 수식들을 순서대로 보시면 푸는 과정 그대로 나타내었기 때문에 이해하시기 좋을 듯 합니다.)
3) LU 분해법을 사용하여 근 구하기
.png)
LU 분해법의 시작은 위와 같은 수식을 만들어주는 것입니다. 우선 제일 위에 식은 문제에서 주어진 그대로를 행렬 표현으로 나타낸 것일 뿐이고, 두번째 줄에 보시면, [A] 행렬이 [L]과 [U]라는 행렬의 곱으로 나타낼 수 있다는 것입니다. 이때의 LU 분해법은 고차행렬의 풀이를 손쉽게 하기 위해 만든 것이고 지금의 문제는 예제 수준이기 때문에 더 복잡해보일 수 있지만, 고차행렬로 가게 되면 더욱 쉽게 풀 수 있다는 장점을 가지고 있습니다.
이때의, [L] 행렬을 2)번에 가우스 소거법을 진행하면서 앞자리 원소를 0으로 만들게하는 '비'의 값이 다음과 같이 나타나고, [U] 행렬은 상삼각행렬로 2)번에서 가우스 소거법을 진행한 마지막 계수행렬이 그대로 사용하게 됩니다.
.png)
이해가 되시나요? 다시 말하자면, [U] 행렬은 가우스 소거법을 통해 만들어진 상삼각행렬이고, [L]행렬은 가우스 소거법을 통해 만들기 위해 중간에 계산된 '비'가 들어간 것입니다. 그리고 [L]의 하삼각행렬의 주대각선은 모두 '1'의 값을 가지게 됩니다. 하나만 예로들면, [L] 행렬의 (2,1)의 원소가 2입니다. 이때의 2는 가우스 소거법에서 2번째 행의 첫 원소를 0으로 만들어주게 되는 '2배'의 숫자 2를 가져온 것입니다.
그렇게 계수행렬 [A]를 분해한 다음, LU 분해법은 다음의 2개의 과정을 거쳐야 합니다.
.png)
1)번은 하삼각행렬 [L]을 통해 새롭게 만들어지게 되는 {d}라는 '새로운' 행렬을 구하게되고, 이를 2)번인 [U]가 포함된 행렬의 결과로 대입하여 {x}의 값을 구하는 것 입니다. 이렇게 하는 이유는 앞에서도 말했듯이 계산은 복잡하지만, 어차피 컴퓨터가 계산하기 때문에 더욱 값을 쉽게 도출하기 위해서 만들어진 방법입니다. 그럼 순서대로 풀어보겠습니다.
.png)
.png)
위에서 말했던 1)번에서 하삼각행렬 [L]을 통해서 새로운 열벡터인 {d}를 구하고 있습니다. 그렇게 구한 열벡터 {d}를 다시 2)번에 상삼각행렬 [U]을 사용하는 수식에 대입하여 문제에서 원하는 근을 구할 수 있습니다.
최종적으로, Cramer 공식, 순수 Guass 소거법, LU 분해법 모두 같은 결과값의 근을 도출하는 것을 보실 수 있습니다. 이 방법은 모두 수치해석에서 선형방정식의 근을 구하는데에 적용되는 풀이법입니다. 이상!
반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
| 【수치해석】 Gauss-Seidel법, Jacobi 반복법 예제 풀이 (7) | 2017.12.20 |
|---|---|
| 수치해석의 이분법과 가위치법 설명 (0) | 2017.11.06 |
| 3x3 행렬식 Determinant 쉽게 구하는 방법 (6) | 2017.11.01 |