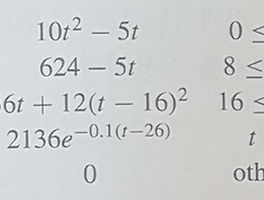반응형
- Chapra의 응용수치해석 3판 연습문제 3.6
[문제]
Q. 2차원 공간상에서 한 점의 위치를 나타내는 데 원점을 기준으로 두 개의 거리가 필요하다.
- 직교좌표계에서 수평과 수직 거리 (x, y)
- 극좌표계에서 반지름과 각도 (r, θ)
극좌표계 (r, θ)를 기초로 하여 직교좌표계를 구하는 것은 상대적으로 간단하다. 그러나 반대 과정은 간단하지 않다. 반지름은 다음 식에 의해 계산된다.
r = (x^2 + y^2)^(1/2)
만약 좌표가 1사분면과 4사분면(즉, x > 0인 경우)에 있다면, θ 를 구하기 위한 간단한 식은 다음과 같다.
θ = atan(y/x)
(참고 atan는 tan의 역함수)
다른 경우에 대해서는 어려움이 야기된다. 다음의 표는 그 가능성을 요약한 것이다.
| x | y |
θ |
<0 |
>0 |
atan(y/x)+π |
<0 |
<0 |
atan(y/x)-π |
<0 |
=0 |
π |
=0 |
>0 |
π/2 |
=0 |
<0 |
-π/2
|
=0 |
=0 |
0 |
r과 θ 를 x와 y 의 함수로 계산하기 위해 if...elseif 구조를 사용하여 M-파일을 작성하라. θ 에 대한 죄종 결과를 각도로 표시하라. 다음의 경우를 계산하여 프로그램을 검증하라.
x |
y |
r |
θ |
2 |
0 |
(이 부분을 구해야함.) |
(이 부분을 구해야함.) |
2 |
1 |
||
0 |
3 |
||
-3 |
1 |
||
-2 |
0 |
||
-1 |
-2 |
||
0 |
0 |
||
0 |
-2 |
||
2 |
2 |
[문제풀이]
먼저, 전체 코드를 보여드리고 설명하겠습니다. 바로 아래가 전체 코드표입니다. 초록색글씨로 약간의 설명을 적어두었습니다.
아래 사진이 위 코드를 실행(F5)한 결과입니다.
이제 차근차근 위에서부터 설명하겠습니다.
우선 1~5번째 줄은 x, y의 주어진 값을 행벡터로 표현하였습니다. 그리고 그때의 r값을 요소별로 제곱(.^)해주어서 반지름(r)을 계산합니다. 이 세개의 변수들은 이렇게 간단하게 함수 첫부분에서 정의하고 시작할 수 있습니다.
그리고 이번 문제에서 중요한 전체 for loop입니다. 그리고 for구문에서 각 요소가 행벡터로 9번째까지 있으므로, for구문용 변수 i를 사용해서 i가 1부터 9까지 반복시켜줍니다. 그리고 내부에 if~elseif 구문을 아래와 같이 사용합니다.
x(i)가 0보다 큰 경우, 작은 경우, 같은 경우로 나눠서 각도(theta)를 구해야하기 때문에 8번째줄부터 시작된 if가 16번째 줄에서 elseif, 18번째 줄에서 else로 나오고 마지막 26번째 줄에서 end로 마치는 구조입니다. 9번째 줄의 if는 15번째 end로 끝이나게 되고, 19번째의 if는 25번째의 end로 구문이 완성되는 구조입니다.
즉, 전체적인 for loop안에, if~elseif가 크게 하나 있고, 그 내부에 if~elseif가 작게 들어가 있는 구조입니다.
추가적으로, 각각의 x, y, theta는 벡터이기때문에 루프구조 내에서 전부다 x(i), y(i), theta(i)로 표현해주어서 벡터로 인식시키게 됩니다.
마지막으로, 결과값을 표현하기 위해서 위와 같이 작성했습니다. 29번째 줄의 disp()는 결과를 보기 편하게 하기 위해서 출력하는 부분이고 30번째 줄의 A행렬은 출력을 위해 임의로 지정하였습니다. 이렇게 출력함수에는 disp(A)처럼 간단히 나타내고 그 위에서 A에 대한 계산을 진행하게되면, 계산시간이 훨씬 많이 단축된다고 합니다. 그렇게 마지막에 disp(A)로 결과를 출력하기 위해서 30번째 줄의 A행렬에서 []를 사욯해서 어퍼스트로피(')를 이용해 행벡터를 열벡터로 치환한 다음 행렬 A로 만들어주었습니다. 그리고 A행렬의 마지막에 theta값은 MALTAB에서는 라디안(radian)단위로 계산하기 때문에 우리가 보기 편하게(그리고 문제에서 원하는 방식인) 각도 단위로 변환해준 것입니다.
그렇게 최종 결과는 위와 같이 실행(F5)됩니다. 1열은 x, 2열은 y, 3열은 r, 4열은 theta(각도단위)로 표현한 것입니다. 이상!
반응형
LIST
'프로그램 > MATLAB' 카테고리의 다른 글
| 【MATLAB】 단순 지지보 특이함수 문제풀이 (11) | 2017.10.02 |
|---|---|
| 【MATLAB】 sin 함수를 무한급수로 푸는 문제 풀이 (0) | 2017.09.30 |
| 【MATLAB】 복리 이자 계산 문제풀이 (0) | 2017.09.30 |