【재료역학】 외팔보 분포하중 문제풀이

실제 공기업에서 필기시험으로 기출되었던 문제입니다. 문제는 외팔보에 얼마인지 모르는 분포하중이 작용하고 있을 때, 허용 굽힘응력을 주어주고 분포하중이 얼마까지 버틸 수 있을지 묻는 문제입니다. 알면 간단하지만, 시간이 지나서 익숙치 않은 개념들이 있다면 못 풀고 넘어갈 수 있을 듯합니다.

[문제]

- 실제 공기업 필기시험 기출문제

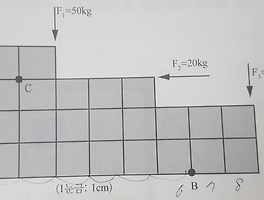
Q. 다음 그림에 주어진 길이 80cm의 외팔보에 자유단으로부터 60cm에 걸쳐 분포하중 q [kgf/cm] 를 작용시키고자 한다. 보의 단면은 직사각형(b x h = 20cm x 30cm) 이고 허용굽힘응력은 50 [kgf/cm^2 으로 할 때 작용시켜야 할 q값을 구하면 얼마인가?

[그림]

[답] 50 [kgf/cm]

[문제설명]

위에서도 말했듯이 그림과 같은 외팔보가 있고 분포하중이 작용하고 있습니다. 이때 분포하중은 크기를 모르는 값인 q라고 나와있고 보의 허용굽힘응력을 주어주고 있습니다. 이 허용응력을 통해서 분포하중 q값을 알아내보라는 문제입니다. 즉, 허용굽힘응력이 주어졌을 때의 보가 버틸 수 있는 분포하중의 크기를 묻고 있습니다. 그리고 분포하중을 그림과 같이 생겼습니다. 분포하중이 받는 범위나 크기가 변위에 따라 달라질 경우에는 아래 문제풀이에서 분포하중 개념만 조금 다르게 적용하여 문제를 풀면 됩니다.

[문제풀이]

우선, 가장 좌측에 고정되어 있는 부분의 반력을 구합니다. 반력의 이름은 R (reaction)이라 하겠습니다. 분포하중이 q [kgf/cm]이기 때문에, 그대로 길이를 곱해주면, 힘평형 때문에 반력의 크기를 알 수 있습니다.

이제 이것이 반력의 크기이자, 분포하중의 크기입니다. 이제 분포하중의 크기를 알았으니, 가해지는 모멘트를 구합니다. (이번 문제에서는 딱히 '반력'이라고 안구해도 됩니다.) 모멘트는 고정단에서부터 분포하중의 중앙부분까지의 거리와 분포하중의 크기를 곱해서 계산할 수 있습니다. 이때, 분포하중은 보의 60cm에 해당하는 부분에 가해지고 있지만, 거리를 곱해줌으로써 분포하중의 가운데 부분에 집중하중이 작용한다고 가정할 수 있습니다. 분포하중을 집중하중으로 교환한 다음에 아래 순서로 문제를 풀어줍니다.

이때, 60q는 분포하중의 크기이며, (20+30)은 고정단에서 분포하중의 중앙까지의 거리입니다.

그리고 문제에서 보의 단면형상을 주어졌습니다. 단면의 형상은 직사각형이고 가로세로 20, 30 cm입니다. 이를 통해 단면계수(Z)를 구합니다.

이제 허용 굽힘응력(sigma)이 주어졌으므로, 아래와 같은 관계로 문제를 풀어줍니다.

이때, 라는 것은 '보의 굽힘응력'을 구하는 공식이 적용되었다는 뜻입니다. 이렇게 분포하중 q를 50 [kgf/cm]로 구했습니다. 이번 문제에서 중요한 공식은 단면계수 Z를 구하는 것과 굽힘응력을 구하는 공식이었습니다. 이상!