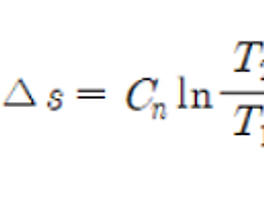안녕하세요. 이전에 작성했었던 포스팅을 다시 재 작성합니다. 사진 속에 있는 링크는 이전에 글을 썻던 블로그 주소입니다. 현재는 해당 블로그는 폐쇄하고 이 블로그를 이용하고 있습니다. 필요하신 정보 얻어가시길 바랍니다.
[문제]
ex3-1) 4-cylinders 2.5L, SI engine operates at WOT on 4-strokes air standard Otto cycle at 3000 rpm, rc=8.6, ηm=86%, S/B=1.025, A/F=15, Q`HV=44,300kJ/kg, ηc=100%. At the start of the compression stroke, P=100kPa, T=60℃, It can be assumed that there is a 4% exhaust residual leftover from the previous cycle.
[해석]
예제3-1) 3000rpm의 오토사이클 4행정으로 2.5리터의 4실린더 SI 엔진이 WOT에서 작동되고있다. 압축비는 8.6, 기계효율은 86%, 스트로크/보어비는 1.025, 공연비는 15, 열유량은 44,300kJ/kg, 압축효율은 100%이다. 압축행정의 시작점에서 압력은 100kPa, 온도는 60℃이다. 그리고 이전 사이클에서 4%의 잔여물이 남아있다.
[풀이]
- 3000 rpm → N=3000/60=50
- Otto cycle 4stroke : 오토(가솔린) 사이클 4행정
- 2.5L : 엔진 전체 용량 = Vd for entire engine
- WOT : wide open throttle, 최대쓰로틀 상태
- rc=8.6 : 압축비
- ηm=86% : 기계효율이 0.86
- S/B=1.025 : stroke = 1.025 x Bore, under square engine
- at the start of the compression stroke, P=100kPa, T=60℃ : 압축행정의 시작점의 압력 100kPa, 온도 60℃=333K, 아래 P-V diagram에서 1번 상태
- 4% exhaust residual leftover from the previous cycle : 이전 행정에서 4%의 잔여물이 남음.
[문제풀이]
sol)
*파란색박스 안의 그래프가 SI엔진의 오토 사이클 P-V diagram이다.
*P-V diagram에서 1,2,3,4번의 위치가 어디인지 정확히 알아야한다. 문제에서 주어진 'At the start of the compression stroke'는 1번 위치이다.
*1번에서 4번으로 가면서 각 과정은
1-2 과정 : 압축행정
2-3 과정 : 폭발행정
3-4 과정 : 팽창행정
4-1 과정 : 배기행정
*T-s diagram도 익혀둘 필요가 있다.
ⅰ) 문제에서 주어진 Vd는 전체 엔진에 대한 displacement volume이다. 문제풀이를 위해 하나의 실린더의 Vd를 구할려면, 문제에서의 Vd for entire engine의 값을 실린더수(4개)로 나눠주면 된다.
따라서, Vd= 2.5/4=0.625 [L]이고 이를 SI단위계로 단위변환하면 0.000625[㎥]이 된다.
(1000L=1㎥)
ⅱ) 문제에서 주어진 압축비(rc)는 8.6이고 이때, 사진에서 보이는 빨간색 박스의 공식을 이용해 Vc를 구한다.
따라서, Vc=82.2 [㎠] : clearance volume
ⅲ) 그리고 문제에서 Vd와 S/B를 주어졌으므로, 각각의 Stroke와 Bore를 구할 수 있다. 관련 공식은 위 사진의 노란색 박스이다.
ⅳ) W(일)을 구하라.
먼저, 각 1번부터 4번 상태의 상태량을 찾아보자.
state 1) 1번 위치의 상태량
- 문제에서 주어진 온도 T = T1이고 60 [℃] = 333 [K] 이다.
- 문제에서 주어진 압력 P = P1이고 100 [kPa] 이다.
- V1은 피스톤이 하사점에 있는 순간의 부피이므로 V1 = Vd + Vc = 0.000707 [㎥] 이다.
- 이때, 이상기체 상태방정식 (PV = mRT)를 사용하여 m을 구한다. m'mix = 0.00074 [kg]
state 2) 2번 위치의 상태량, 1-2 과정은 등엔트로피, 압축행정이므로
- P2 = P1 (rc)^k = 1826 [kPa] : 등엔트로피일때의 관련 공식사용
- T2 = T1 (rc)^k = 707 [K] : 등엔트로피일때의 관련 공식사용
- V2는 이상기체 상태방정식(PV = mRT)를 이용하면 V2 = 0.0000822 [㎥]
- V2를 구하는 다른 방법은 압축비를 이용하거나 상사점일때의 부피를 구하면 된다. (위 사진 참조)
state 2) 이어서)...
이때, 공연비를 알고 있고 문제에서 exhaust rasidual이 4%라고 했으므로,
m`mix에 공연비를 곱하면 m`air,
m`mix에 연공비를 곱하면 m`fuel,
m`mix에 4%를 곱하면 m`exhaust rasidual 값이 나오게된다.
이는 각각의 행정마다 실린더 내에 들어가는 공기, 연료, 잔여물의 유동질량이다.
state 3) 3번의 상태량, 2-3 과정 : 폭발행정
- 위 사진의 빨간색 박스가 보이는가. 그 공식이 아주 중요한데, 내연기관 문제에서 압축행정 이후의 온도를 구하는데 용이하게 쓰인다. (이때, Cv는 정적비열이다.)
따라서, T3 = 3915 [K]이고 이는 T`max이다. (T3 = T`max)
- V3 = V2와 같다. (= V`TDC)
- P3는 위 사진의 파란색 박스의 공식을 사용하여 구한다. 열역학 강의때 배운 공식이다.
state 4) 3-4과정 : 등엔트로피 팽창행정
- 팽창할때, 이론적으로는 엔트로피의 변화는 없다.
- T4와 P4는 등엔트로피 관련 열역학 공식을 이용하여 구한다. (위 사진의 빨간색 박스들)
- P-V diagram에서도 알 수 있듯이 V4 = V1이다. (=V`BDC)
이때, 압축일과 팽창일을 계산해보자.
- 파란색 박스 : 팽창일 구하기.
- 빨간색 박스 : 압축일 구하기.
해당 일을 구할때는, 'W = mCvΔT [kJ]'를 이용하여 구한다.
따라서, 전체 엔진이 하는 순수한 일은
W'net,indicated = (1-2과정의 work) + (3-4과정의 work) = 1.03 [kJ]
그리고 예제 3-1의 문제에서 추가적으로 구할 수 있는 것들을 구해보자.
공식만 알면 쉽게 풀수 있는 문제들이다. 내연기관의 공식들 중 안외워도 되는 공식은 없다. 필히 전부다 암기하고 문제풀이에 임할 수 있도록한다.
ⅰ) 지시열효율
(지시열효율) = (지시일) / (열) 로 구하거나,
(지시열효율) = 1 - 1/(압축비)^k-1 로 구한다. (이 공식은 열역학 공식을 내연기관의 압축비를 이용하여 표현한 식이다. 3장 수업시간에 배운다. 단, 검산용으로만 사용할 것.)
ⅱ)imep [kPa]
imep = (지시일) / Vd 로 구한다.
ⅲ) indicated power
(indicated power) = (work) x (rpm) 으로 구한다. 위 사진의 빨간색 박스와 표현만 다를뿐 동일한 공식이다.
ⅳ) mean piston speed
mean piston speed 구하는 공식 사용
ⅴ) brake work
brake work은 indicated work에 기계효율을 곱하면된다.
(ηm = brake work / indicated work)
ⅵ) brake torque
brake torque는 위 사진의 빨간색 박스 안의 두가지 공식 중 하나를 이용하여 구한다. 필히 암기해야하는 공식이므로 설명 생략.
ⅶ) 삭제
ⅷ) friction power
friction power = indicated power - brake power 으로 구한다.
(friction 상태량 = indicated 상태량 - brake 상태량)
ⅸ) bmep
bmep = ηm x imep로 구한다.
(ηm = bmep / imep [kW])
또는 bmep = Wb / Vd로 구한다. (bmep의 정의)
ⅹ)bsfc (brake specific fuel consumption)
bsfc = m`fuel / brake power로 구한다. (bsfc 정의)
ⅹⅰ) ηv (volumetric efficiency, 흔히 체적/용적효율이라 부른다.)
ηv = m`a / (ρ`a x Vd) 을 이용하여 구한다.
그리고 마지막으로, 이전 블로그에서 댓글을 통해 질문&답변이 이루어진 부분도 사진으로 게시합니다.
'공학 문제해결 > 열역학' 카테고리의 다른 글
| [내연기관] 3-4 문제풀이, L6 CI 엔진 (0) | 2017.07.22 |
|---|---|
| 【열역학】폴리트로픽 polytropic 변화에서의 공식, 관계식, 절대일, 공업일, 열량, 비열, 엔트로피 변화량 (0) | 2017.07.10 |
| 【열역학】[지식in답변] N/mm^2을 ksi 단위로 환산/변환하는 방법 (0) | 2017.07.08 |