반응형
안녕하세요. 이번 포스팅에서는 이차 곡선(원, 타원, 쌍곡선, 포물선)에서 기울기가 m인 접선의 방정식을 구해보고 그림을 통해 이해해보는 시간을 가지려고 합니다. 순서는 1번 원, 2번 타원, 3번 쌍곡선, 4번 포물선 순으로 작성하였으니 참고하시길 바랍니다. 궁금하신 점은 언제나 댓글을 이용해주시면 감사하겠습니다.
1. 원
기울기가 m인 직선의 방정식  와 원
와 원  가 접할 때를 생각한다.
가 접할 때를 생각한다.
원의 중심인  과 직선
과 직선  의 거리가 반지름
의 거리가 반지름  과 같음을 이용한다.
과 같음을 이용한다.
2. 타원
기울기가 m인 직선의 방정식  와 타원
와 타원  가 접한다.
가 접한다.
따라서 타원의 접선의 방정식은 
P.S.
원 또한 같은 방법으로 구할 수 있다.
그리고 원 또한 타원의 특수한 형태로 생각해볼 수 있다.
⇒ 타원 공식을 활용해 원의 접선을 구해도 된다.
3. 쌍곡선
타원과 비슷하다.
4. 포물선
접하는 직선의 방정식을  라 설정한다.
라 설정한다.
끝!
반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
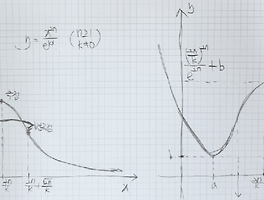
| 【수학】 수능에 자주 등장했던 초월함수 그래프 그리기 (0) | 2018.08.11 |
|---|---|
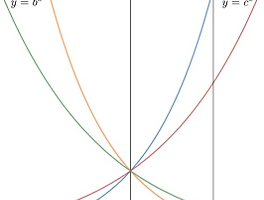
| 간단한 지수함수와 로그함수의 밑 대수비교 (0) | 2018.07.15 |
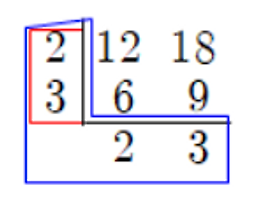
| 최대공약수, 최소공배수 쉽게 구하는 방법 (0) | 2018.07.15 |