반응형
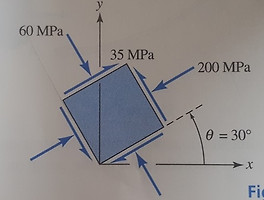
[문제]
[문제해설]
재료역학에서 외팔보 문제입니다. 단, 익숙치 않은 꺽여있는 외팔보 형태이지만 살짝만 생각하면 간단하게 풀 수 있는 문제입니다. 꺽여있는 부분에 집중 하중이 작용하고 있는데, B점에서의 처짐이 0이 되기 위한 CD(a)의 거리를 a/L처럼 거리비의 형태로 묻고 있습니다.
[답]
[풀이 및 설명]
우선, 점 A는 벽에 고정되어있는 고정단입니다. 점 D에 집중하중 P가 작용하여 외팔보에 응력이 작용할 것입니다. 문제에서 점 B의 변위가 0이 되게 하라했으니, 점B에 대해서 보겠습니다.
하중 P로 인해 점 B에는 아래와 같은 힘과 모멘트가 발생하게 됩니다. 이는, 힘을 힘과 모멘트로 변환(이동)하는 정역학에 대한 개념입니다. 힘을 옮기게되면 그 힘과 동시에 옮기는 변위만큼의 작용하는 모멘트가 추가되게 됩니다. 힘의 크기는 P로 동일하며, 힘의 이동이 발생함으로 모멘트 M=aP가 생기게 됩니다.
그럼 점 B에서의 힘과 모멘트로 인해 변위가 발생하게 됩니다. 힘은 아래로 작용하기 때문에 점B를 아래로 당기고 있고, 모멘트는 시계방향이기때문에 점B를 위로 당기고 있습니다. 힘이 일정하므로 모멘트의 크기 변화로 인해 점 B의 변위가 0이 되게 만들 수 있습니다. 그러므로 a는 아래와 같은 풀이로 답을 얻을 수 있습니다.
우선, 집중하중의 경우 외팔보의 처짐은  이고, 모멘트가 작용할 경우 외팔보의 처짐은
이고, 모멘트가 작용할 경우 외팔보의 처짐은  입니다. 이제 변위가 0이므로,
입니다. 이제 변위가 0이므로,  의 관계를 만족해야합니다. 즉,
의 관계를 만족해야합니다. 즉,  로 두고 문제를 풀어도 됩니다. 두 변위가 방향이 반대이므로 +와 - 의 부호는 신경쓰지 않아도 됩니다.
로 두고 문제를 풀어도 됩니다. 두 변위가 방향이 반대이므로 +와 - 의 부호는 신경쓰지 않아도 됩니다.
(신경쓴다면 델타1은 아래니까 - 부호이고, 델타2는 위방향이니까 + 부호입니다.)
그럼 문제는 이렇게 풀 수 있습니다.
1)  의 형태로 둘 수 있고
의 형태로 둘 수 있고
2)  에서 양변의 같은 물리량을 소거하면
에서 양변의 같은 물리량을 소거하면
3)  가 됩니다.
가 됩니다.
즉, 답은 문제에서 묻고 있는 거리비의 형태인 a/L로 나타낸  가 됩니다.
가 됩니다.
[개념]
- 브라켓 = 외팔보 = TV를 벽이나 천장 등에 고정시키기 위해 TV와 벽면을 연결시켜주는 철재 부속품입니다. TV 기종에 따라 설치할 수 있는 사이즈나 벽면 재질에 따른 설치 가능 여부 확인해야 합니다.
- 정역학에서 힘의 이동
-
집중하중일 때, 외팔보의 처짐 =
-
모멘트일 때, 외팔보의 처짐 =
- [역학문제 해결/재료역학] - 재료역학 핵심이론 속성강좌 추천
[프로그램/Ansys] - 집중하중이 작용하는 양단 고정보 Ansys Static Structural 해석 연습
[자격증/일반기계기사] - 일반기계기사 1과목 재료역학 기출 키워드 정리
반응형
LIST
'공학 문제해결 > 재료역학' 카테고리의 다른 글
| 【재료역학】 푸아송 비 문제 풀이 (0) | 2017.08.08 |
|---|---|
| 【재료역학】 경사단면의 경사각 구하는 문제 풀이 (0) | 2017.08.03 |
| 【재료역학】 질량관성모멘트의 평행축 정리, 예제문제 풀이 (0) | 2017.07.28 |