대학 4학년 1학기는 어떻게 보냈는지 나중에 알아보려고 도서관을 다닐 때마다 밑에 사진처럼 자리표를 끈어서 보관했었습니다. 결과는 3월달 0개, 4월달 31개, 5월달 23개, 6월달 20개였습니다. 1학기 전체 통틀어서 총 74번 도서관을 갔네요. 1학기 총 일수가 107일이었던 것을 감안하면, 1.446일마다 도서관을 갔네요. 지난 한 학기동안 학점은 12학점 밖에 안들었지만, 일반기계기사 자격증 공부나 졸업논문을 공부하거나, 독서하거나 기타 등등 여러가지 공부를 하러 아주 열심히 다녔네요. ㅎㅎ 제 자신에게 칭찬하고 싶은 날입니다. 앞으로도 열공하면서 열심히 포스팅하는 모습 지켜봐주시고 자주 방문해주시면서 아낌없는 조언 부탁드립니다^^


radian과 도(˚)를 서로서로 변환하는 방법입니다.
흔히 알고 있는 원은 360(˚)입니다. 이를 수학 및 공학에 자주 사용하는 단위인 radian으로 바꿔주면 이 됩니다. 이제 이 관계를 아래와 같이 수식으로 표현할 수 있습니다.
위 1~2)번에서 "360도(˚)는이다."라는 한국말을 수식으로 여러 형태로 표현한 것입니다. 1)번에서는 도(˚)를 radian 단위로 표현하고 있고 (참고에서는 1도를 라디안으로 표현), 2)번에서는 라디안 단위를 각도로 표현하고 있습니다. 이제 이를 이용해서 아래에 있는 예제 문제 풀이를 보시면서 변환은 어떻게 하는 것인지 알아보겠습니다.
위 예제를 잘 봐주시길 바랍니다. 예제 1)번에서는 각도를 라디안으로 바꿔주고 있습니다. 각도를 소거해주면서 라디안으로 바꾸기 위해 
이상! 오늘 하루도 열공하시길 바라고, 파이팅하세요~^^
'공학 문제해결 > 수학' 카테고리의 다른 글
| 【수학】 삼각함수 공식 쉽게 외우는 방법 (sin, cos, tan, cosec, sec, cot) (0) | 2017.07.13 |
|---|---|
| 【수학】회전관련 단위 rad/s ↔ rpm 단위 변환하기 (0) | 2017.07.08 |
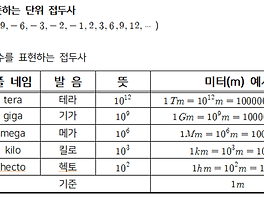
| 수학,공학. 10의 x배를 뜻하는 단위 접두사 (hecto,kilo,mega,giga,tera,deci,centi,milli,micro,nano) (2) | 2017.07.08 |