반응형
"어떤 비관론자도 별의 비밀을 발견하거나, 미지의 섬으로 항해하거나, 인간정신의 새로운 낙월을 연 적이 없다."
- 헬렌 켈러
안녕하세요. 이번 포스팅에서는 재료역학에서 '집중하중이 작용하는 외팔보'의 처짐과 처짐각에 대한 문제풀이입니다. 아주 기본적인 문제이지만, 기사시험을 비롯한 곳에서는 최종적으로 답이되는 공식들만을 암기해야합니다...ㅠㅜ 포스팅 보시고 도움이 되서 파이팅하시길 바랍니다!!
[문제]
그림과 같은 외팔보의 자유단의 처짐은 얼마인가? (단, EI는 일정하다.)
[문제풀이]
외팔보 자유단에 집중하중 P가 작용하고 있는 상태입니다. 이때, 좌측 고정단에는 반력 R과 반모멘트 M이 형성됩니다.
(아래 그림 참조. 그림은 1년여전에 그린게 있어서 사진 찍었습니다. 못생긴건 이해부탁드립니다.)
위와 같이 반력 R과 반모멘트 M을 그릴 수 있고 바로 구할 수 있습니다. 반력 R은 하중이 P밖에 없기 때문에 방향은 반대이고 크기는 동일(R = P)합니다. 그리고 고정단의 반모멘트도 역시나 집중하중 P로 인한 모멘트밖에 없기 때문에 방향은 반대이고 크기는 동일한 M = PL이 됩니다.
(위 문제에서는 길이를 소문자 l로 표현했고, 풀이에서는 구분하기 쉽게 대문자 L로 표현하겠습니다.)
그리고 BMD (굽힘 모멘트 선도)를 위와 같이 그릴 수 있습니다. 이때, 고정단에서의 거리를 x라고 하면 위와 같이 반모멘트식은 Px - PL이 됩니다. 그리고 처짐의 개념을 이용해서 아래와 같이 풀이할 수 있습니다.
1)에서는 처짐의 개념을 이용해서 바로 적용한 것이고,
2)와 3)은 부정적분을 시행한 것입니다.
4), 5)번은 각각 2), 3)번 식에 경계조건(B.C. : boundary condition)을 적용하여 부정적분 상수값을 구해준 것입니다.
따라서,
처짐각 y'은 2-1)처럼 구할 수 있고, 이를 정리하면 2-2)가 됩니다.
처짐량 y는 3-1)처럼 구할 수 있고, 이를 정리하면 3-2)가 됩니다.
이제 위에서 구한 2-2)와 3-2)식에 자유단(x = L)에서의 처짐각과 처짐량을 아래와 같이 구할 수 있습니다.
즉, 처짐각은 y'에 x = L을 대입한 2-3)이 답이 되고,
처짐량은 y에 x = L을 대입한 3-3)이 답이 됩니다.
[답]
이상!
반응형
LIST
'공학 문제해결 > 재료역학' 카테고리의 다른 글
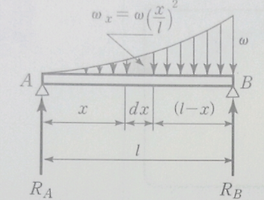
| 【재료역학】 단순보 비균일 분포하중 문제풀이 (3) | 2018.04.02 |
|---|---|
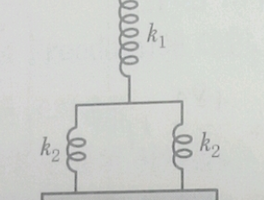
| 【기계진동】 용수철-질량계 고유진동수 문제풀이 (0) | 2018.03.29 |
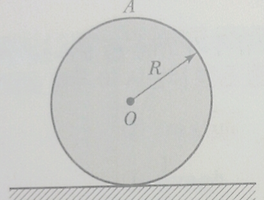
| 【동역학】 바퀴의 순간중심 문제풀이 (3) | 2018.03.29 |