반응형
"극복할 장애와 성취할 목표가 없다면 우리는 인생에서 진정한 만족이나 행복을 찾을 수 없다." - 맬스웰 몰츠
안녕하세요. 이번에는 재료역학에서 단순보에 비균일 분포하중이 작용할 때에 단순보의 반력을 구해보는 문제를 풀어보겠습니다. 총 2개의 문제를 가지고 와서 풀었으니, 더 적합한 풀이 예시를 보시고 공부에 도움이 되시길 바랍니다. ①번 문제는 비균일 분포하중이 x에 대한 함수로 주어진 경우이며, ②번 문제는 비균일 분포하중이 사다리꼴 형태로 주어진 문제입니다.
[문제 ①]
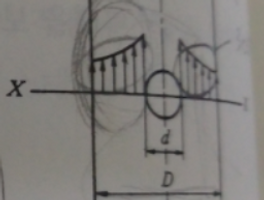
그림과 같은 단순보(simple beam)의 A 지점의 반력은 얼마인가?
[문제풀이]
위 그림은 단순보이며, 하중으로 비균일 분포하중이 작용하고 있습니다. 이때, 반력을 구하는데, 반력은 A, B점에 각각 수직방향으로 작용하는 2개의 힘뿐입니다. 아래와 같이 힘평형, 모멘트 평형을 적용하면서 분포하중을 적분해주게되면 문제를 풀 수 있습니다. 이때, 분포하중은 x에 대한 함수로 주어졌습니다.
우선, 힘 평형조건을 사용합니다.
이렇게 반력 R`A, R`B의 합을 구하였습니다.
다음으로, 모멘트 평형을 적용합니다.
위와 같이, 모멘트 평형으로 R`B를 구하고 위에서 구했던 식에 대입하여 R`A도 구할 수 있습니다. 위에서 모멘트 평형을 계산하면서 비균일 분포하중의 무게중심을 찾기위해서 무게중심의 정의가 사용되었습니다.
- 무게중심 정의 :
[답]
따라서, A점의 반력은  입니다.
입니다.
다음 문제를 풀어보겠습니다.
[문제 ②]
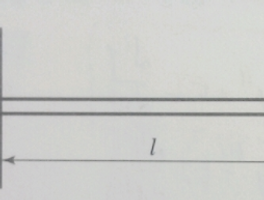
길이 l = 10m 의 단순보(simple beam)에 단위 ω = (3x+5) N/m로 표시되는 분균일 분포하중이 작용할 때 보의 반력 R`A를 구하여라.
[문제풀이]
이번 문제도 좌측 점 A의 반력을 구하는 문제입니다. 다만, 위의 문제와는 조금 다른 것이 분포하중의 비균일 정도입니다. 위 문제에서는 분포하중이 x에 대한 함수로 주어졌지만, 이번에는 직접 그 값을 숫자식으로 계산해야합니다. 사다리꼴의 넓이를 구할 수 있어야 하고, 삼각형의 도심을 구할 수 있어야 합니다.
먼저, 분포하중부터 해석해보겠습니다. 분포하중의 크기는 다음과 같이 사다리꼴의 넓이로 계산할 수 있습니다.
그리고 분포하중(사다리꼴 = 삼각형 + 사각형)의 도심을 구합니다.
이때, 삼각형의 도심은 높이의 1/3이라는 것은 상식이라 생각하고 바로 적용했다는 점 참고해주시길 바랍니다. 이렇게 분포하중에 대한 해석을 마치고, 이번 문제의 반력을 구하기 위해서 '힘 평형과 모멘트 평형'을 아래와 같이 적용합니다.
힘 평형에서는 위와 같이 분포하중의 크기(200N)가 적용되었습니다.
그리고 모멘트 평형을 적용합니다.
위와 같이 모멘트 평형을 적용하여 B점에서의 반력은 75N이라는 것을 알 수 있고, 또한 위에서 구한 힘 평형 방정식에서 A점의 반력은 125N이라는 것도 알 수 있습니다. 이상!
[답]
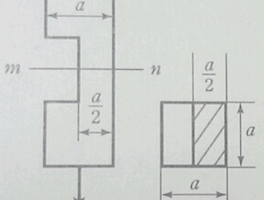
【재료역학】 가운데가 빈 중공축 면적, (극)관성모멘트, (극)단면계수 구하는 방법
반응형
LIST
'공학 문제해결 > 재료역학' 카테고리의 다른 글
| 【재료역학】 기둥 전체응력 문제풀이 (1) | 2018.04.03 |
|---|---|
| 【재료역학】 집중하중 외팔보의 처짐 및 처짐각 (0) | 2018.03.31 |
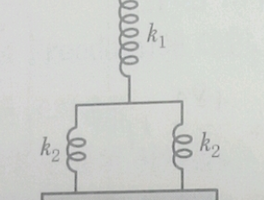
| 【기계진동】 용수철-질량계 고유진동수 문제풀이 (0) | 2018.03.29 |