반응형
"There is only one success - to be able to spend your life in your own way." - Christopher Morley
"오직 한 가지 성공이 있을 뿐이다. 바로 자기 자신만의 방식으로 삶을 살아갈 수 있느냐이다." - 크리스토퍼 몰리
안녕하세요. 이번 포스팅에서는 고등학교 수학 수준에서 '평면운동'을 이해해보겠습니다.
고등학교 수학 수준에서 평면운동은 일반적으로 시간에 따른 x축의 위치 변화와 시간에 따른 y축의 위치 변화를 계산합니다. 시간에 따른 z축의 계산이 포함되면 공간운동이 되겠습니다.
비교적 쉽게 이해하기 위해 예를 들자면, 바둑판과 바둑돌을 생각해봅시다. 바둑판의 정중앙 즉 천원[天元]을 원점으로 생각하고, 그 곳에 검은 돌을 둡니다. 만약 시간에 따라(1초 마다) 가로로 1만큼 세로로 2만큼 움직인다면, 검은 돌은 (1,2) 지점으로 이동을 하게 됩니다.
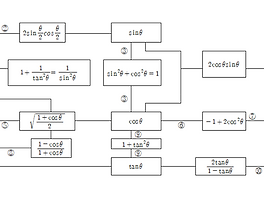
관계식을 만들어 보면,  가 됩니다.
가 됩니다.
검은 돌을 이동시키지 않고 계속 놓아본다면  의 그래프 모양대로 놓아지기도 하겠군요. 이처럼 시간에 따른 변수로서 위치를 표시하게는 것이 가장 기초입니다.
의 그래프 모양대로 놓아지기도 하겠군요. 이처럼 시간에 따른 변수로서 위치를 표시하게는 것이 가장 기초입니다.
그렇다면  는 어떻게 표시될까요?
는 어떻게 표시될까요?
따라서,  로 나타내어집니다.
로 나타내어집니다.
더 나아가,  입니다.
입니다.
따라서  는
는  로 나타내어집니다.
로 나타내어집니다.
즉 예시의 처음에 움직인 바둑돌의 시간에 따른 위치는  이고, 속도는 (1, 2), 그리고 가속도는 (0, 0)이 되겠습니다.
이고, 속도는 (1, 2), 그리고 가속도는 (0, 0)이 되겠습니다.
P.S. 속도는 벡터 값으로 방향이 표기됩니다.
속력은 방향이 표시되지 않는 값으로 스칼라 값이라고 합니다. 따라서 속도와 속력은 엄연히 다른 표기법을 가지며, 서로 다른 개념으로 접근해야합니다.
평면운동에서 속도의 개념은 x축 이동과 y축 이동을 따로 표시하는 순서쌍으로 등장하지만, 속력은 그 크기를 계산한 숫자로 등장합니다.
위치의 미분이 속도가 되듯 속도의 적분은 위치가 됩니다.
비슷하게, 속력의 적분은 이동거리가 되겠습니다.
따라서  입니다.
입니다.
㈎ 
위 의 식에서

㈏  ← [ 곡선의 길이 공식 ]
← [ 곡선의 길이 공식 ]
곡선의 길이 공식이나 이동거리의 계산식이나 같은 것을 알 수 있습니다.
P.S.
㈎  [모두 벡터 값]
[모두 벡터 값]
㈏ 

반응형
LIST
'공학 문제해결 > 수학' 카테고리의 다른 글
| 【수학】 삼각형의 도심 (0) | 2018.07.12 |
|---|---|
| 【수학】 정적분과 급수 쉽게 풀어보기 + 예제 (0) | 2018.06.30 |
| 【수학】 정적분과 급수, 곱셈공식 이용 문제풀이 (0) | 2018.06.30 |