기계공학에서 재료역학 문제들 중 자주 나오는 중공축 (속이 비어 있는 축)의 면적과 관성모멘트, 극관성모멘트, 단면계수를 구해보겠습니다.
우선, 중공축의 정의를 보겠습니다.
네이버 도해 기계용어사전에서는 "축의 자중(自重)을 가볍게 하기 위해 단면의 중심부에 구멍이 뚫려 있는(중공[中空]) 축. 속을 비워도 중심축에 비해 강도는 그만큼 감소하지 않는다."라고 정의하고 있습니다.
중공축은 중실축보다 재료를 덜 사용하지만, 여러가지 조건(단면계수 등)을 살펴봤을때에 더 효율적인 설계가 가능하다는 장점 때문에 기계제품, 건설현장 등에 많이 쓰입니다.
1. 중공축 면적구하기

우선, 중공축을 간단하게 그려보면 위와 같습니다. (그림실력은 아무도 못 알아준다죠?)
이때, 외경을 Dout라 하고 내경을 Din이라 하겠습니다.
참고로, 중실축은 중공축과 대비되는 단어로 일반적으로 가득차 있는 원이라고 생각하시면 편합니다.
※ 중공축 = 구멍파인 원 : 중앙 부분이 비어(공)있는 축
※ 중실축 = 완전한 원 : 중앙 부분까지 가득(실)차있는 축
면적은 위와 같이 구할 수 있습니다. 중학교 시절 때 부터 배웠던 원의 면적이 중실축의 면적이고, 안에 있는 비어있는 공간의 면적을 빼주게되면 중공축의 면적이 됩니다.
* 원의 면적 = π D^2 / 4
* 중공축의 면적 = π ( Dout^2 - Din^2 ) / 4
2. 중공축 관성모멘트 구하기
관성모멘트는 I로 표현하며, 원의 경우에 I는 πD^4 / 64 입니다. 이때, 중공축은 면적을 구할때와 마찬가지로 가운데 부분을 빼주면 됩니다. 아주 쉽죠?
3. 중공축 극관성모멘트(=단면2차모멘트) 구하기
극 관성모멘트는 관성모멘트 Ix와 Iy의 합입니다. 따라서 위와 같이 표현 됩니다.
※ Ip = Ix + Iy
4. 중공축 단면계수 구하기
단면계수(Z)는 I/e 입니다. 이때 e는 중심에서 끝점까지의 거리를 나타냅니다. 극 단면계수(Zp)는 위에 공식에 I대신 Ip를 넣어주면 됩니다. (모르겠으면 댓글 남겨주세요.)
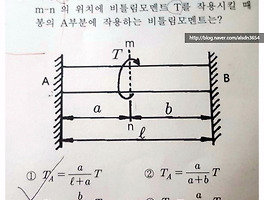
+) 관련 예제 (일반기계기사 기출문제)
아래는 일반기계기사에서 기출되었던 문제들 중, 중공축 넓이 구하기 관련된 문제입니다. 해설까지 나와있으니 이해하는 겸 눈으로 풀어보시길 바랍니다! (아직 응력을 안 배우셨다면, 안 보는걸 추천....드립니다.)
[역학문제 해결/재료역학] - 【재료역학】 질량관성모멘트의 평행축 정리, 예제문제 풀이
[역학문제 해결/재료역학] - 재료역학 핵심이론 속성강좌 추천
[역학문제 해결/재료역학] - 【재료역학】평행축 정리 + 관성 모멘트 문제 풀이
'공학 문제해결 > 재료역학' 카테고리의 다른 글
| 【재료역학】 질량관성모멘트의 평행축 정리, 예제문제 풀이 (0) | 2017.07.28 |
|---|---|
| 【재료역학】 양단이 고정된 봉의 비틀림 문제 풀이 (0) | 2017.07.26 |
| 【재료역학】 단위 체적당 탄성변형에너지 예제문제 풀이 (2) | 2017.07.26 |